Até agora, estudamos a análise BJT dependente do nível de β sobre seus pontos de operação correspondentes (ponto Q). Nesta discussão, verificaremos como determinadas condições de circuito podem ajudar na determinação da possível faixa de pontos de operação ou pontos Q e no estabelecimento do ponto Q real.
O que é Análise de Linha de Carga
Em qualquer sistema eletrônico, a carga aplicada em um dispositivo semicondutor geralmente produzirá um impacto significativo no ponto de operação ou na região de operação de um dispositivo.
Se for feita uma análise por meio de um desenho gráfico, poderíamos traçar uma linha reta cruzando as características do dispositivo para estabelecer a carga aplicada. A interseção da linha de carga com as características do dispositivo pode ser usada para determinar o ponto de operação ou o ponto Q do dispositivo. Esse tipo de análise é, por razões aparentes, conhecida como análise de linha de carga.
Como implementar a análise de linha de carga
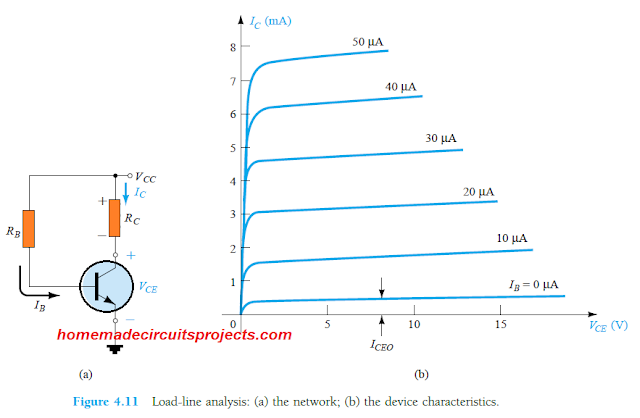
O circuito mostrado na Figura 4.11(a) a seguir determina uma equação de saída que fornece uma relação entre as variáveis IC e VCE conforme mostrado abaixo:
VCE = VCC – CICV (4.12)
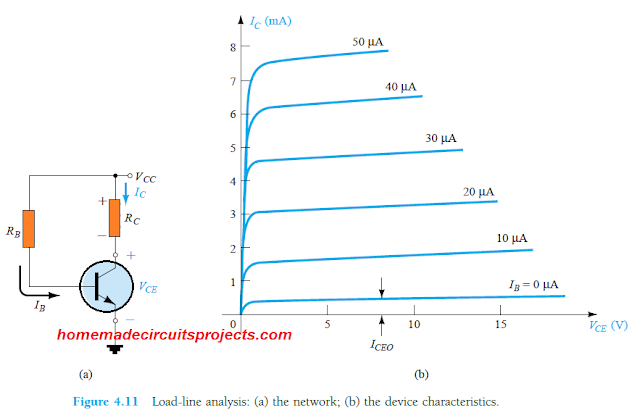
Alternativamente, as características de saída do transistor mostradas no diagrama (b) acima também fornecem a relação entre as duas variáveis IC e VCE.
Isso essencialmente nos ajuda a obter uma equação baseada em diagrama de circuito e uma gama de características através de uma representação gráfica que funciona com variáveis semelhantes.
O resultado comum dos dois é estabelecido quando as restrições definidas por eles são cumpridas simultaneamente.
Alternativamente, isso pode ser entendido como soluções sendo alcançadas a partir de duas equações concorrentes, onde uma é configurada com a ajuda do diagrama de circuitos, enquanto a outra das características do datasheet do BJT.
Na Fig. 4.11b podemos ver as características IC vs VCE do BJT, então agora podemos sobrepor uma linha reta descrita pela Eq (4.12) sobre as características.
O método mais fácil de traçar a Eq (4.12) sobre as características poderia ser executado pela regra que diz que qualquer linha reta é determinada por dois pontos distintos.
Selecionando IC = 0mA, descobrimos que o eixo horizontal se torna a linha onde um dos pontos toma sua posição.
Também substituindo IC = 0mA na Eq (4.12), obtemos:
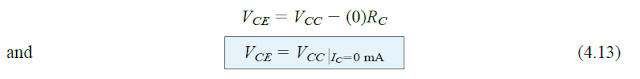
Isso determina um dos pontos para a linha reta, conforme indicado na fig 4.12 abaixo:
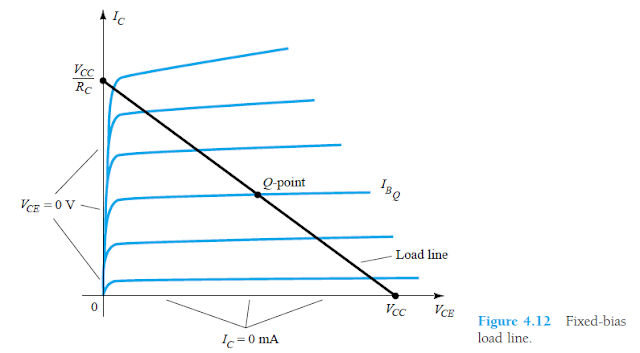
Agora, se escolhermos VCE = 0V, isso configura o eixo vertical como a linha onde nosso segundo ponto assume sua posição. Com esta situação, agora podemos descobrir que IC pode ser avaliada pela seguinte equação.
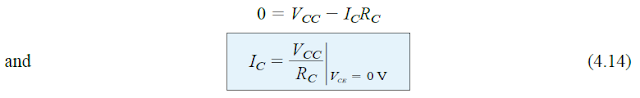
o que pode ser claramente testemunhado na Fig. 4.12.
Ao conectar os dois pontos conforme determinado pelas Eqs. (4.13) e (4.14), uma linha reta estabelecida pela Eq 4.12 pode ser traçada.
Esta linha vista no gráfico Fig 4.12 é reconhecida como a linha de carga uma vez que é caracterizado pelo resistor de carga RC.
Ao resolver o nível estabelecido de IB, o ponto Q real pode ser fixado conforme mostrado na Fig 4.12
Se variarmos a magnitude de IB variando o valor de RB, encontraremos os deslocamentos do ponto Q para cima ou para baixo ao longo da linha de carga, conforme ilustrado na Fig. 4.13.
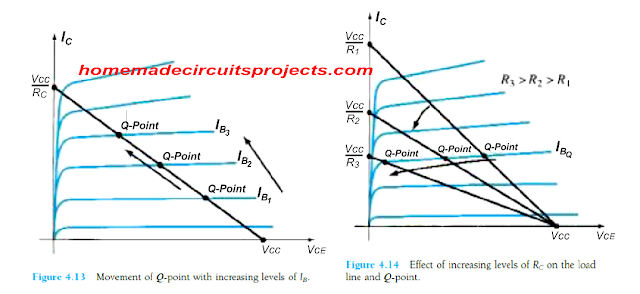
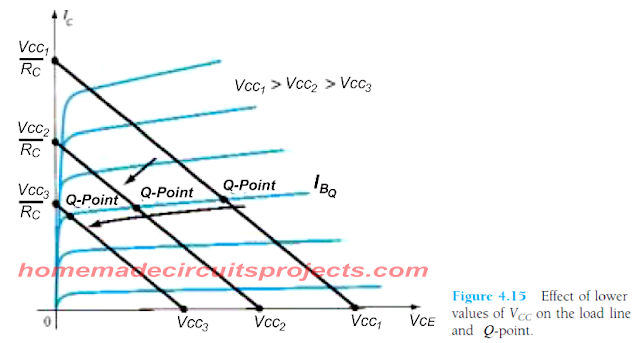
Se mantivermos um VCC constante e alterarmos apenas o valor de RC, encontraremos o deslocamento da linha de carga conforme indicado na Fig 4.14.
Se mantivermos IB constante, encontraremos o ponto Q mudando sua posição conforme indicado na mesma figura 4.14.
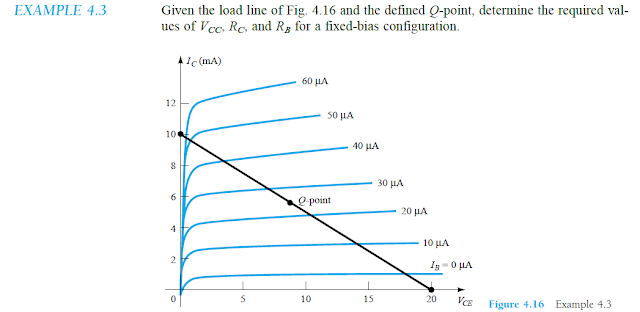
Resolvendo um Exemplo Prático de Análise de Linha de Carga

Referência: https://en.wikipedia.org/wiki/Load_line_(electronics)
Hashtags: #Análise #linha #carga #circuitos #BJT
FONTE
Nota: Este conteúdo foi traduzido do Inglês para português (auto)
Pode conter erros de tradução
Olá, se tiver algum erro de tradução (AUTO), falta de link para download etc…
Veja na FONTE até ser revisado o conteúdo.
Status (Ok Até agora)
Se tiver algum erro coloque nos comentários