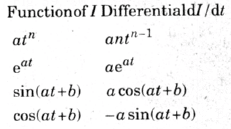Os indutores podem ser imaginados como o oposto dos capacitores. A principal diferença entre um capacitor e um indutor é que um capacitor carrega um dielétrico de proteção entre suas placas, o que inibe a condução de corrente através de seus terminais. Aqui funciona como um circuito aberto.
Por outro lado, a indutância de um indutor é normalmente (embora nem sempre) de resistência incrivelmente baixa ou mínima. Ele se comporta essencialmente como um circuito fechado.
Dualidade do Indutor do Capacitor
Existe um termo único em eletrônica para este tipo de relação entre dois parâmetros de um circuito ou partes de um circuito. Os elementos deste tipo de par são conhecidos como duais um do outro. Por exemplo, dependendo da capacidade de conduzir corrente, um circuito aberto é o duplo de um circuito fechado.
No mesmo princípio, um indutor é o dual de um capacitor. A dualidade de indutores e capacitores é muito mais profunda do que apenas a capacidade natural de conduzir corrente.
Neste artigo, comparamos o princípio de funcionamento do indutor e do capacitor e avaliamos os resultados com cálculos e fórmulas.
Apesar do fato de que os indutores normalmente raramente são vistos em circuitos eletrônicos, já que hoje em dia são substituídos principalmente por ampolas em filtros ativos), as outras partes envolvidas em um circuito parecem carregar alguma quantidade de indutância.
A auto-indutância dos terminais de um capacitor ou resistor torna-se um grande problema em circuitos de alta frequência, o que explica por que os resistores e capacitores de montagem em superfície sem chumbo são tão frequentemente empregados em tais aplicações.
Equações Básicas de Capacitores
A equação fundamental para capacitores é aquela com a qual o farad é definido:
C = Q/I [Eq.19]
onde C é a capacitância em farad, Q é a carga em coulomb e U é o pd entre as placas em volts.
Através da Eq. 19, obtemos uma fórmula da forma Q = ∫ I dt + c onde c é a carga inicial, se disponível. Tendo identificado Q, podemos determinar U a partir da Eq. 19:
U = 1 / C ∫ I dt + c/ C [Eq.21]
Uma característica importante de um capacitor pode ser assim, se uma corrente periódica é aplicada a ele (geralmente uma corrente que oscila senoidalmente), a carga no capacitor e a tensão através dele também flutuam senoidalmente.
A curva de carga ou tensão é uma curva cosseno negativa, ou podemos imaginá-la como uma curva senoidal que fica atrás da curva de corrente por π/2 rad (90°).
A equação fundamental que define o Henry, a unidade de indutância, é
L = NΦ / I [Eq.22]
Com referência a uma única bobina, a auto-indutância em Henry pode ser a relação de fluxo (o fluxo magnético <1) em Weber multiplicado pelo número de enrolamento N, (porque o fluxo magnético corta cada espira), quando uma corrente unitária passa por ele (I = 1 A). Uma definição ainda mais prática pode ser extraída da Eq. 22, usando a equação de Neumann. Este afirma que:
U = N (dΦ / dt) [Eq.23]
O que esta equação sugere é o fato de que a fem induzida dentro de um indutor é relativa à taxa de variação do fluxo ligada.
Quanto mais rápido o fluxo varia, maior a fem induzida Por exemplo, quando o fluxo sobre o indutor ou bobina aumenta a uma taxa de 2 mWb s-1 e supondo que a bobina tenha VINTE E CINCO voltas, então U = 25×2 = 50V.
O caminho da fem é tal que resiste às variações de fluxo conforme delineado pela Lei de Lenz.
Essa verdade é muitas vezes apontada precedendo o lado direito da equação com um sinal de menos, no entanto, enquanto acreditarmos que U é a fem traseira, o sinal pode ser removido.
Diferenciais
O termo dΦ/dt na Eq. 23 indica o que aprendemos como a taxa de variação do fluxo. A frase é chamada de diferencial de Φ em relação a t, e um ramo inteiro da aritmética é dedicado a trabalhar com esse tipo de expressão. A frase tem a forma de um único número (dΦ) dividido por mais uma quantidade (dt).
Diferenciais são utilizados para associar vários conjuntos de proporções: dy/dx, por exemplo, correlaciona as variáveis x e y. Quando um gráfico é plotado usando valores de x no eixo horizontal e valores de y no eixo vertical, dy/dx significa quão íngreme é a inclinação, ou gradiente, do gráfico.
Se U é a tensão porta-fonte do FET, onde T é a corrente de dreno relacionada, então dI/dU significa a quantidade com a qual I varia para determinadas mudanças em U. Alternativamente, podemos dizer que dI/dU é a transcondutância. Ao discutir indutores, dΦ /dt pode ser a taxa de variação do fluxo com o tempo.
O cálculo de um diferencial pode ser considerado como o procedimento inverso da integração. Não há espaço adequado neste artigo para examinar a teoria da diferenciação, no entanto, vamos definir uma tabela de grandezas comumente usadas junto com seus diferenciais.
Diferenciais padrão
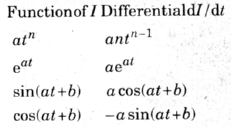
A tabela acima funciona usando I e t como os fatores em vez da rotina x e y. Para que seus detalhes sejam especificamente pertinentes à eletrônica.
Como exemplo, considerando que I= 3t +2, a forma como I se desvia em relação ao tempo pode ser visualizada no gráfico da Fig. 38. Para encontrar a taxa de variação de I em qualquer momento, estimamos dI/dt, por referindo-se à tabela.
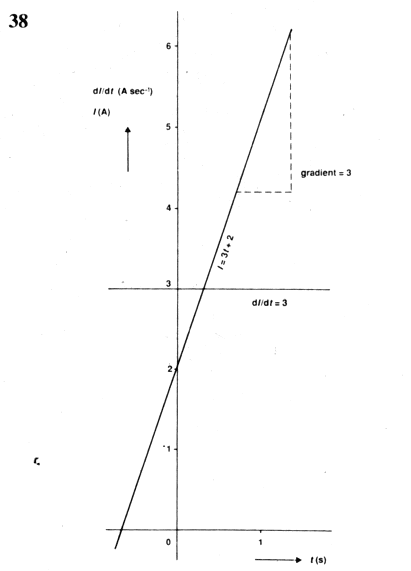
O primeiro elemento da função é 3t ou, para formatá-lo como a primeira linha da tabela, 3t1 . Sen = 1, o diferencial é 3t1-1 = 3t0.
Desde t0 = 1, o diferencial é 3.
A segunda quantidade é 2, que pode ser expressa como 2t0 .
Isso muda n = 0, e a magnitude do diferencial é zero. O diferencial de uma constante será sempre zero. Combinando os dois, temos:
dI/dt = 3
Nesta ilustração o diferencial não inclui t, o que significa que o diferencial não depende do tempo.
Simplificando, a inclinação ou gradiente da curva na Fig. 38 é 3 continuamente o tempo todo. A Figura 39 abaixo mostra a curva para uma função diferente, I = 4 sen 1,5t.
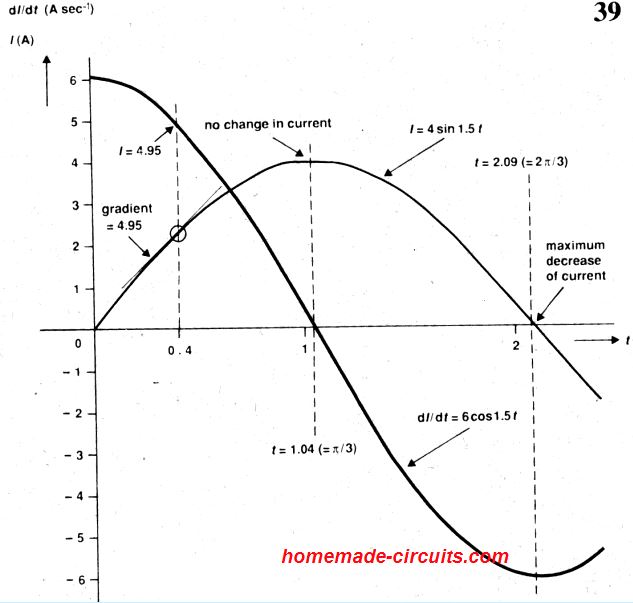
Com referência à tabela, α = 1,5 eb = 0 nesta função. A tabela mostra, dl/dt = 4×1,5cos1,5t = 6cos 1,5t.
Isso nos informa a taxa instantânea de variação de I. Por exemplo, em t = 0,4, dI/dt = 6cos0,6 = 4,95. Isso pode ser observado na Fig. 39, na qual a curva para 6 cos0,6t inclui o valor 4,95 quando t = 0,4.
Também podemos observar que a inclinação da curva 4sin1.5t é 4,95 quando t = 0,4, como mostra a tangente à curva nesse ponto (em relação às diferentes escalas nos dois eixos).
Quando t = π/3, um ponto em que a corrente é máxima e constante, neste caso dI/dt = 6cos(1,5xπ/3): 0, correspondendo a variação zero da corrente.
Ao contrário, quando t = 2π/3 e a corrente está alternando no nível mais alto possível de positivo para negativo, dI/dt = 6cosπ = -6, vemos seu maior valor negativo, exibindo uma alta redução de corrente.
O simples benefício dos diferenciais é que eles nos permitem determinar taxas de variação para funções que são muito mais complexas em comparação com I = 4s em 1,5t, e sem ter que plotar as curvas.
Voltar para Cálculos
Reorganizando os termos da Eq 22, obtemos:
Φ = (L / N)I [Eq.24]
Onde L e N têm dimensões constantes, mas Φ e I podem ter valor em relação ao tempo.
Diferenciando os dois lados da equação em relação ao tempo dá:
dΦ / dt = (L / N) (dI / dt) [Eq. 25]
Mesclando esta equação com a Eq.23 dá:
U = N(L/N)(dI / dt) = L (dI / dt) [Eq.26]
Esta é outra forma de expressar a Henrique. Podemos dizer que, uma bobina com autoindutância de 1 H, uma variação de corrente de 1 A s-1 gera uma fem de retorno de 1 V. Dada uma função que define como uma corrente varia com o tempo, a Eq. 26 nos ajuda a calcule a fem traseira de um indutor em qualquer instante.
Seguem alguns exemplos.
A) I= 3 (uma corrente constante de 3 A); dl/dt = 0. Você não pode encontrar nenhuma mudança de corrente, portanto, a fem traseira é zero.
B) I = 2t (corrente de rampa); dI/dt = 2 A s-1. Com uma bobina transportando L = 0,25 H, a fem traseira será constante em 0,25 x 2 = 0,5 V.
C) I = 4sin1.5t (a corrente senoidal dada na ilustração anterior; dl/dt = 6cos 1.5t. Dada uma bobina com L = 0.1 H, a fem traseira instantânea é 0.6cos1.5t. A fem traseira segue o diferencial curva da Fig. 39, mas com amplitude de 0,6 V em vez de 6 A.
Entendendo as “duplas”
As duas equações a seguir significam a equação de um capacitor e indutor, respectivamente:
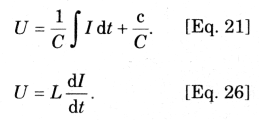
Isso nos ajuda a determinar o nível de tensão produzido no componente pela corrente variando no tempo de acordo com uma função específica.
Vamos avaliar o resultado obtido por diferenciando os lados L e H da Eq.21 em relação ao tempo.
dU / dt = (1 / C)I
Como sabemos que a diferenciação é o inverso da integração, a diferenciação de ∫I dt inverte a integração, ficando apenas I como resultado.
Diferenciar c/C resulta em zero e reorganizar os termos produz o seguinte:
I = C.dU / dt [Eq.27]
Isso nos permite saber o sentido da corrente se está indo em direção ao capacitor ou saindo dele, em resposta a uma tensão que varia de acordo com uma determinada função.
O interessante é que o acima equação da corrente do capacitor parece semelhante à equação de tensão (26) de um indutor, que exibe a capacitância, dualidade de indutância.
Da mesma forma, a diferença de corrente e potencial (pd) ou a taxa de variação da corrente e pd podem ser duais quando aplicadas a capacitores e indutores.
Agora, vamos integrar a Eq.26 em relação ao tempo para completar o quarteto de equações:
∫ U dt+c = LI
A integral de dI/dt é = I , reorganizamos as expressões para obter:
I = 1/L∫ U dt + e/L
Isso novamente se parece bastante com a Eq.21, provando ainda mais a natureza dual da capacitância e indutância, e seu pd e corrente.
Até agora, temos um conjunto de quatro equações que podem ser usadas para resolver problemas relacionados a capacitores e indutores.
Por exemplo, a Eq.27 pode ser aplicada para resolver o problema como este:
Problema: Um pulso de tensão aplicado em 100uF produz uma curva conforme mostrado na Fig abaixo.
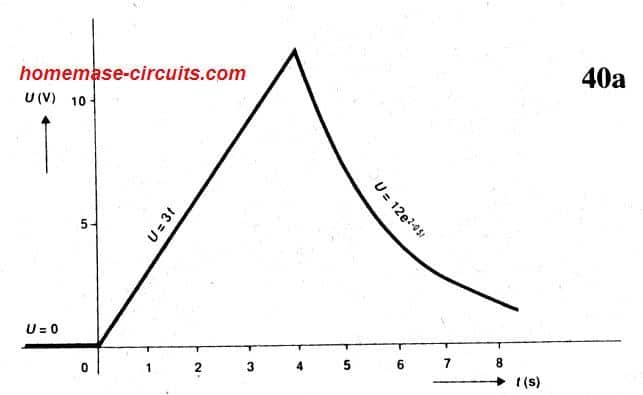
Isso pode ser definido usando a seguinte função por partes.

Calcule a corrente que se move através do capacitor e trace os gráficos correspondentes.
Solução:
Para o primeiro estágio aplicamos a Eq.27
I = C(dU / dt) = 0
Para a segunda instância em que U pode estar subindo com uma taxa constante:
I = C(dU / dt) = 3C = 300μA
Isso mostra uma corrente de carga constante.
Para o terceiro estágio quando U cai de forma exponencial:
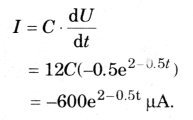
Isso indica que a corrente flui para fora do capacitor em uma taxa exponencial decrescente.
Relação de Fase
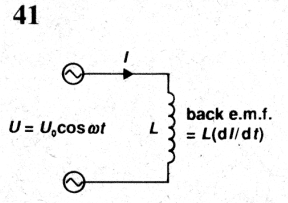
Na figura abobe, um pd alternado é aplicado a um indutor. Este pd em qualquer instante pode ser expresso como:
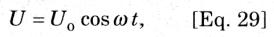
Onde Uo é o valor de pico do pd. Se analisarmos o circuito na forma de um loop e aplicarmos a lei de Kirchhoff das tensões no sentido horário, obtemos:
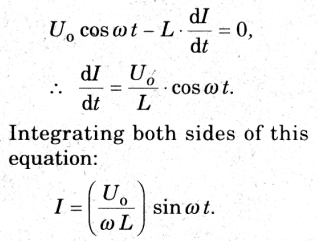
No entanto, como a corrente é senoidal aqui, os termos entre colchetes devem ter o valor igual à corrente de pico Io, portanto, finalmente obtemos:
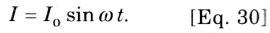
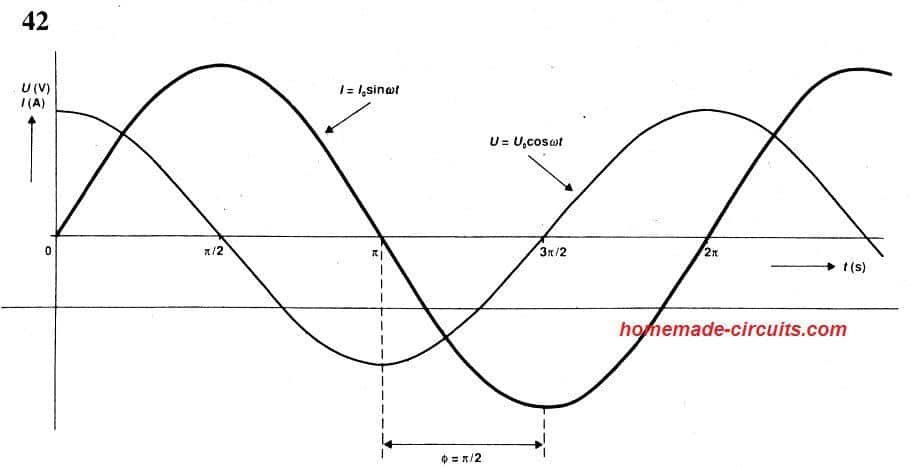
Se compararmos a Eq.29 e a Eq.30, descobrimos que a corrente I e a tensão U têm a mesma frequência, e I fica atrás de U em π/2.
As curvas resultantes podem ser estudadas no diagrama a seguir:
C
Isso mostra a relação contrastante entre capacitor e indutor. Para uma corrente de indutor está atrasada em relação à diferença de potencial em π/2, enquanto para um capacitor, a corrente está adiantada em relação a pd. Isso mais uma vez demonstra a natureza dual dos dois componentes.
Hashtags: #Cálculos #indutor #capacitor
FONTE
Nota: Este conteúdo foi traduzido do Inglês para português (auto)
Pode conter erros de tradução
Olá, se tiver algum erro de tradução (AUTO), falta de link para download etc…
Veja na FONTE até ser revisado o conteúdo.
Status (Ok Até agora)
Se tiver algum erro coloque nos comentários